Rational Polarization Can Be Profound, Persistent, and Predictable

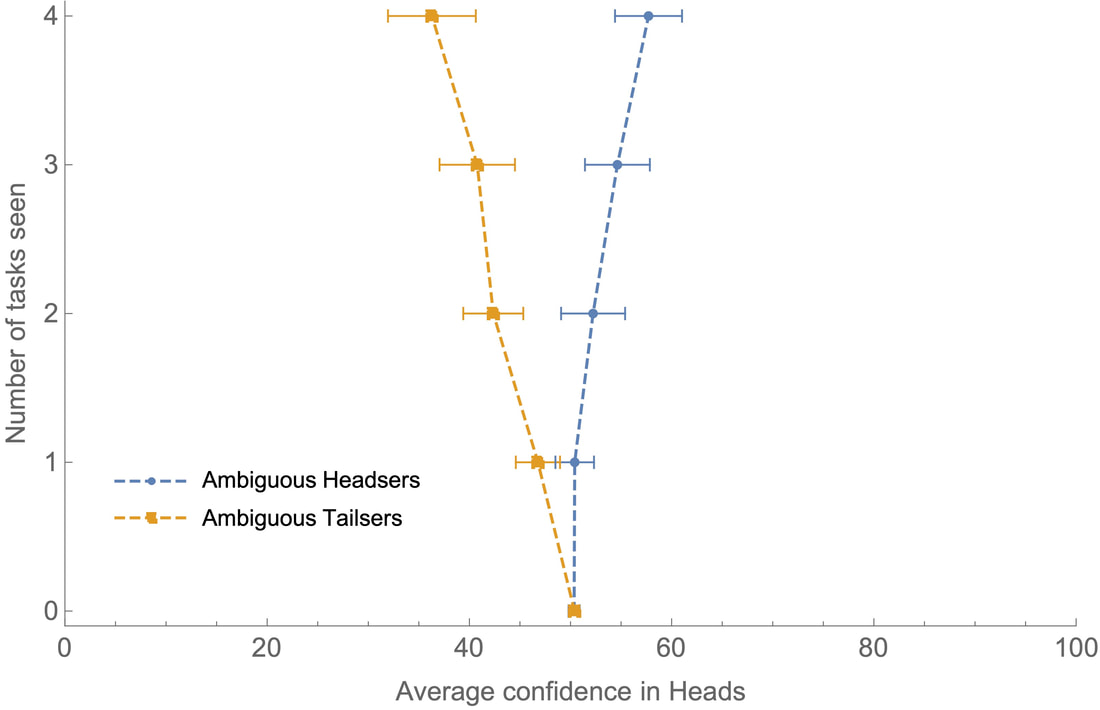
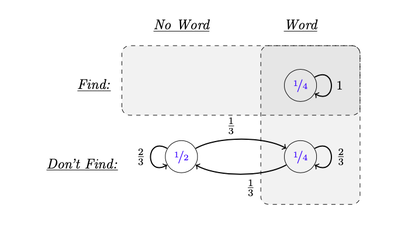
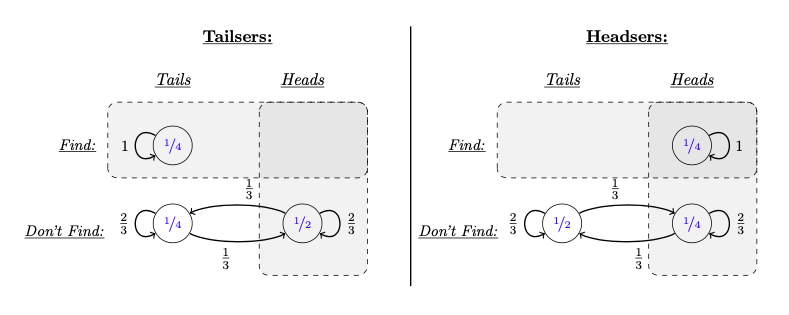
(2000 words; 9 minute read.)

So far, I’ve laid the foundations for a story of rational polarization. I’ve argued that we have reason to explain polarization through rational mechanisms; showed that ambiguous evidence is necessary to do so; and described an experiment illustrating this possibility.

Today, I’ll conclude the core theoretical argument. I'll give an ambiguous-evidence model of our experiment that both (1) explains the predictable polarization it induces, and (2) shows that such polarization can in principle be profound (both sides end up disagreeing massively) and persistent (neither side is changes their opinion when they discover that they disagree).

With this final piece of the theory in place, we’ll be able to apply it to the empirical mechanisms that drive polarization, and see how the polarizing effects of persuasion, confirmation bias, motivated reasoning, and so on, can all be rationalized by ambiguous evidence.

Recall our polarization experiment. 

I flipped a coin, and then showed you a word-completion task: a series of letters and blanks that may or may not be completable by an English word.  For example, FO_E_T is completable (hint: where are there lots of trees?); but _AL_W is not (alas, Bernhard Salow is not yet sufficiently famous).
​
One group—the Headsers—saw a completable string if the coin landed heads; the other group—the Tailsers—saw a completable string if the coin landed tails. As they did this for more and more tasks, their average confidence that the coins landed heads diverged more and more:

Question: what drives this polarization—and why think that it is rational?

Our word-completion task provides an instance of what is sometimes called a “good-case/bad-case asymmetry” in epistemology (Williamson 2000, Lasonen-Aarnio 2015, Salow 2018). The asymmetry is that you get better (less ambiguous) evidence in the “good” case than in the “bad” case—and, therefore, it’s easier to recognize that you’re in the good case (when you are) than to recognize that you’re in the bad case (when you are).

In our experiment, the “good case” is when the letter-string is completable; the “bad case” is when it’s not. The crucial fact is that it’s easier to recognize that a string is completable than to recognize that it’s not.  It’s possible to get unambiguous evidence that the letter-string is completable (all you have to do is find a word). But it’s impossible to get unambiguous evidence that it’s not completable.

In particular, what should you think when you don’t find a word?  This is some evidence that the string is not completable—but how much? After all, you can’t rule out the possibility that you should find a word, or that you should at least have an inkling that there’s one. More generally, you should be unsure what to make of this evidence: if there is a word, you have more evidence that there is; if there’s not, you have less; but you can’t be sure of which possibility you’re in.

There are a variety of models we can give of your evidence to capture this idea, all of which satisfy the value of evidence and yet lead to predictable polarization (see the Technical Appendix (§5.1) for some variations).

Here's a simple one:

Either there is a word, or there’s not; and either you find one, or you don’t—but you can’t find a word that’s not there, so there are only 3 types of possibilities (the circles in the diagram).

The numbers inside the circles indicate how confident you should be, beforehand, that you’ll end up in those possibilities: you should be ½ confident that there’ll be no word (and you won’t find one), since that’s determined by a coin flip; and if there is a word, there’s some chance (say, ½) you’ll find one, meaning you should be ½*½ = ¼ confident you’ll end up in each of the Word-and-Find (top right) and Word-and-Don’t-Find (bottom right) possibilities.

Meanwhile, the labeled arrows from possibilities represent how confident you should be after you see the task, if in fact you’re in that possibility. 

If there's a word and you find one, you should be sure of that—hence the arrow labeled “1” pointing from the top-right possibility to itself. If there’s no word and you don’t find one, you should be somewhat confident of that (say ⅔ probability), but you should leave open that there’s a word that you didn’t find (say, ⅓ probability).  But if there is a word and you don’t find one, you should be more confident than that—after all, since there is a word, you’ve received more evidence that there is, even if that evidence is hard to recognize. Any higher number will do, but in this model you should be ⅔ confident there’s a word if there is one and you don't find one.

If you don’t find a word, your evidence is ambiguous because you should be unsure how confident you should be that there’s a word—maybe you should be ⅓ confident; maybe instead you should be ⅔ confident. (In a realistic model there would be many more possibilities, but this simple one illustrates the structural point.)

There are two important facts about this model: (1) it is predictable polarizing, and yet (2) it satisfies the value of evidence.

Why is the evidence predictably polarizing? You start out ½ confident there’ll be a word. But you prior estimate for how confident you should end up is higher than ½. After all, there’s a ½ chance your confidence should go up—perhaps way up, perhaps only somewhat up. Meanwhile, there’s a ½ chance it should go down—but not very far down.  Thus, on average, you expect seeing word-completion tasks to provide evidence that there’s a word.

(Precisely: your prior expectation of the posterior rational confidence is ½*⅓ + ¼*⅔ + ¼*1 = 7/12, which is greater than ½.)

Notice that if you had unambiguous evidence—so that the rational confidence was the same at all possibilities wherein you don’t find a word—this model would not be predictably polarizing. (Then your prior expectation would be ¾*⅓ + ¼*1 = ½.)

So what drives the predicable polarization is the ambiguity—in particular, the fact that when you don’t find a word, you should be more confident the string is completable if there is a word than if there’s not.

This, incidentally, is empirically confirmed: in my experiment, amongst tasks in which people didn’t find a word (had confidence <100%), the average confidence when there was no word was 44.6%, while the average confidence when there was a word was 52.3%—a statistically significant difference. (Stats: t(309) = 2.77, one-sided p = 0.003, and d=0.32.)

Why is the evidence valuable, despite being polarizing? Note that the rational posterior degrees of confidence are uniformly more accurate than the prior rational confidence: no matter what possibility is actual, you become uniformly more confident of truths and less confident of falsehoods. 

This can be seen by noting that, in each possibility, the probabilities always become more centered on the actual possibility. For example, suppose there’s no word. Then initially you should be ½ confident of this, and afterwards you should be ⅔ confident of it. Conversely, suppose there is a word. Then initially you should be ½ confident of this, but afterwards you should be either ⅔ confident of it (bottom right), or certain of it (top right). And so on.

Because of this, the model satisfies the value of evidence: no matter what decision about the word-completion task you might face, you should prefer to get the evidence before making your decision. (Proof in the Technical Appendix, §5.1.)

(700 words left)

Profound, Persistent Polarization

How, in principle, could this type of evidence lead to profound and persistent polarization?

First note what happens when we divide people into Headsers and Tailsers: we give them symmetric, mirror-image types of evidence. Headsers see completable strings when the coin lands heads; Tailsers see them when it lands tails. Thus Headsers tend to get less ambiguous evidence when the coin lands heads, while Tailsers tend to get less ambiguous evidence when the coin lands tails:

As a result, Headsers should become (on average) more confident in heads, while Tailsers should become (on average) more confident of tails.

​(Precisely: although both start out ½ confident of heads, on average Headsers should be 1/6 more confident of heads than Tailsers should be.)

Now consider: what happens if we present each group with a large number of independent word-completion tasks.  (For simplicity, imagine they all know that they’re 50% likely to find a word if there is one, so they don’t learn anything new about their abilities as they proceed.)

Each time they’re presented with a word-completion task, they face a question: “On this toss, will I find a word, and will the coin land heads or tails?”  Since the coin tosses are each fair and independent, the answer to all of these questions are independent: knowing the answers to some of them has no bearing on the others. Moreover, we’ve seen that with respect to each one of these questions, the evidence is valuable.

In fact, more is true.  Let $Q$ be the question "How will each of the coins land?" By iterating this process in the right way, we can make it such that at each stage $i$ of the process, you should expect that the evidence you'll receive about coin $i+1$ is valuable with respect to $Q$.  (This, mind you, is the most subtle philosophical and technical step—see the Technical Appendix, §5.2, for more discussion.)

Thus at each time, if what you care about is getting to the truth about how any of the coins landed, you should gather the evidence.
​
Suppose Headsers and Tailser both do this.  Then it will predictably lead to profound and persistent disagreement.

Why?  By the weak law of large numbers, everyone can predict with confidence that Headsers should wind up very confident that around 7/12 (≈58%) of the coins landed heads, while Tailsers should wind up very confident that around 5/12 (≈42%) of the coins did.

Now consider the claim:

    Mostly-Heads: more than 50% of the coins landed heads.

Everyone can predict, at the outset, that Headsers will become very confident (in fact, with enough tosses, arbitrarily confident) that Mostly-Heads is true, and Tailsers will become very confident it’s false.

​​Thus we have profound polarization.

Moreover, even after undergoing this polarization, Headsers will still be very confident that Tailsers will be very confident that Mostly-Heads is false; meanwhile, Tailsers will be very confident that Headsers will be very confident that Mostly-Heads is true. As a result, neither group will be surprised—and thus neither group will be moved—when they discover their disagreement.

Thus we have persistent polarization.

In short: the ambiguity-asymmetries induced by the sort of evidence presented in word-completion tasks can be used to lead rational people to be predictably, profoundly, and persistently polarized. (See the Technical Appendix, §5.2, for the formal argument.)

This completes the theoretical argument of this series: the type of polarization we see in politics—polarization that is predictable, profound, and persistent--could be rational.

The rest of the series will make the case that it is rational. In particular, I’ll argue that this ambiguity-asymmetry mechanism plausibly helps explain the empirical mechanisms that drive polarization: persuasion, confirmation bias, motivated reasoning, etc.

It’s not hard to see, in outline, how the story will go.

For “heads” and “tails” substitute bits of evidence for and against a politically contentious claim—say, that racism is systemic. Recall how Becca and I went our separate ways in 2010—I, to a liberal university; she, to a conservative college.

I, in effect, became a Headser: I was exposed to information in a way that made it easier to recognize evidence in favor of systemic racism. She, in effect, became a Tailser: she was exposed to information in a way that made it easier to recognize evidence against systemic racism.

If that were what happened, then both of us could've predicted that we would end up profoundly polarized—as we did. And neither of us should be moved now when we come back and discover our massive disagreements—as we’re not.

And yet: although we each should think that the other is wrong, we should not think that they are less rational, or smart, or balanced than we ourselves are.

That is the schematic story of how our polarized politics could have resulted from rational causes.

In the remainder of this series, I’ll argue that it has.


What next?
If you liked this post, consider signing up for the newsletter, following me on Twitter, or spreading the word.
For the formal details underlying the argument, see the Technical Appendix (§5).
Next post: How confirmation bias results from rationally avoiding ambiguity.