|
(This post is co-written with Matt Mandelkern, based on our joint paper on the topic. 2500 words; 12 minute read.)
It’s February 2024. Three Republicans are vying for the Presidential nomination, and FiveThirtyEight puts their chances at:
Some natural answers: "Pence"; "Pence or Carlson"; "Pence, Carlson, or Haley". In a Twitter poll earlier this week, the first two took up a majority (53.4%) of responses:
But wait! If you answered "Pence", or "Pence or Carlson", did you commit the conjunction fallacy? This is the tendency to say that narrower hypotheses are more likely than broader ones––such as saying that P&Q is more likely than Q—contrary to the laws of probability. Since every way in which "Pence" or "Pence or Carlson" could be true is also a way in which “Pence, Carlson, or Haley” would be true, the third option is guaranteed to be more likely than each of the first two.
Does this mean answering our question with “Pence” or “Pence or Carlson” was a mistake? We don’t think so. We think what you were doing was guessing. Rather than simply ranking answers for probability, you were making a tradeoff between being accurate (saying something probable) and being informative (saying something specific). In light of this tradeoff, it’s perfectly permissible to guess an answer (“Pence”) that’s less probable––but more informative––than an alternative (“Pence, Carlson, or Haley”). Here we'll argue that this explains––and partially rationalizes––the conjunction fallacy. 1. Good Guesses We make guesses whenever someone poses a question and we can’t be sure of the answer. “Will it rain tomorrow?”, “I think it will”; “What day will the meeting be?”, “Probably Thursday or Friday”; “Who do you think will win the nomination?”, “I bet Pence will”; and so on. What sorts of guesses are good guesses? The full paper argues that there are a variety of robust and intricate patterns, drawing on a fascinating paper by Ben Holguín. Here we’ll just focus on the main patterns in our lead example. Suppose you have the probability estimates from above (Pence, 44%; Carlson, 39%; Haley, 17%), and we ask you: “Who do you think will win?” As we've seen, a variety of answers seem reasonable: (1) "Pence" ✓ (2) "Pence or Carlson" ✓ (3) "Pence, Carlson, or Haley" ✓ In contrast, a variety of answers sound bizarre: (4) "Carlson" ✘ (5) "Carlson or Haley ( = "Not Pence") ✘ (6) "Pence or Haley" ✘ We’ve run examples like this by dozens of people, and the judgments are robust––for instance, in a similar Twitter poll in which "Pence or Haley" was an explicit option, it was the least-common answer (6.7%):
What’s going on? How do we explain why (1)–(3) are good guesses and (4)–(6) are bad ones?
Our basic idea is a Jamesian thought: making good guesses involve trading off two competing goals. On the one hand, we want to avoid error––to be accurate. On the other, we want to get at the truth––to be informative. These two goals compete: the more informative your guess, the less likely it is to be true. A good guess is one that optimizes this tradeoff between accuracy and informativity. More precisely, we assume that guesses have answer values that vary with their accuracy and informativity. True guesses are better than false ones, and informative true guesses are better than uninformative true ones. Given that, here’s our proposal: Guessing as Maximizing: In guessing, we try to select an answer that has as much answer-value as possible––we maximize expected answer-value. To make this precise, we can clarify the notion of informativity using a standard model of a question. Questions can be thought of as partitioning the space of open possibilities into a set of complete answers. For example: the set of complete answers to “Will it rain tomorrow?” is {it will rain, it won’t rain}; the set of complete answers to “Who will win the nomination?” is {Pence will win, Carlson will win, Haley will win}; and so on. In response to a question, a guess is informative to the extent that it rules out alternative answers. Thus “Pence” is more informative than “Pence or Carlson”, which in turn is more informative than “Pence, Carlson, or Haley”. Given this, we can explain why (4)–(6) are bad guesses. Consider “Carlson”. It's exactly as informative as “Pence“––both rule out 2 of the 3 possible complete answers––but it is less probable: “Carlson“ has a 39% chance of being true, while “Pence” has a 44% chance. Thus if you’re trying to maximize expected answer value, you should never guess “Carlson”, since “Pence” is equally informative but more likely to be accurate. Similarly, consider “Pence or Haley”. What’s odd about this guess is that it “skips” over Carlson. In particular, if we swap “Haley” for "Carlson”, we get a different guess that's equally informative but, again, more probable. (“Pence or Carlson” is 44 + 39 = 83% likely to be true, while “Pence or Haley” is 44 + 17 = 61% likely.) On the other hand, the Guessing as Maximizing account explains why (1)–(3) can all be good guesses. The basic point: if you really care about being informative, you should choose a maximally specific answer (“Pence”); if you really care about being accurate, you should choose a maximally likely answer (“Pence, Carlson, or Haley”); and intermediate ways of weighting these constraints lead to good guesses at intermediate levels of informativity (“Pence or Carlson”). (For a formal exposition of all this, see the Appendix or the paper.)
(1400 words left)
3. The conjunction fallacy
With this account of guessing in hand, let’s apply it to our opening observation: guessing leads to the conjunction fallacy. Recall: this is the tendency to rate narrower hypotheses (like “P&Q”) as more probable than broader ones (like “Q”). It’s the star of the show in the common argument that people’s reasoning is systematically irrational, lacking an understanding of the basic rules of probability and instead using simple heuristics. The most famous example is from the original paper by Tversky and Kahneman: Linda is 31 years old, single, outspoken and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations. Which of the following is more likely?
A majority of subjects said “feminist bank teller” (FT) was more probable than “bank teller” (T). Again, this violates the laws of probability: every possibility in which Linda is a feminist bank teller is also one in which she’s a bank teller––but not vice versa.
What’s going on here? Our proposal: Answer-Value Account: People commit the conjunction fallacy because they rank answers according to their quality as guesses (their expected answer-value), rather than their probability of being true. In other words, we think the Linda case is analogous to the following one: It’s 44% likely that Pence will win, 39% likely that Carlson will, and 17% likely that Haley will. Which of the following are you more inclined to guess?
Given the above survey, we can expect that around half of people would choose (a). (Since 35/(35 + 38.2) = 47.8%.) The crucial point is that in both the Linda and Pence cases, option (a) is less probable but more informative than option (b) with respect to the salient question––e.g. “What are Linda’s social and occupational roles?” or “Who will win the nomination?”
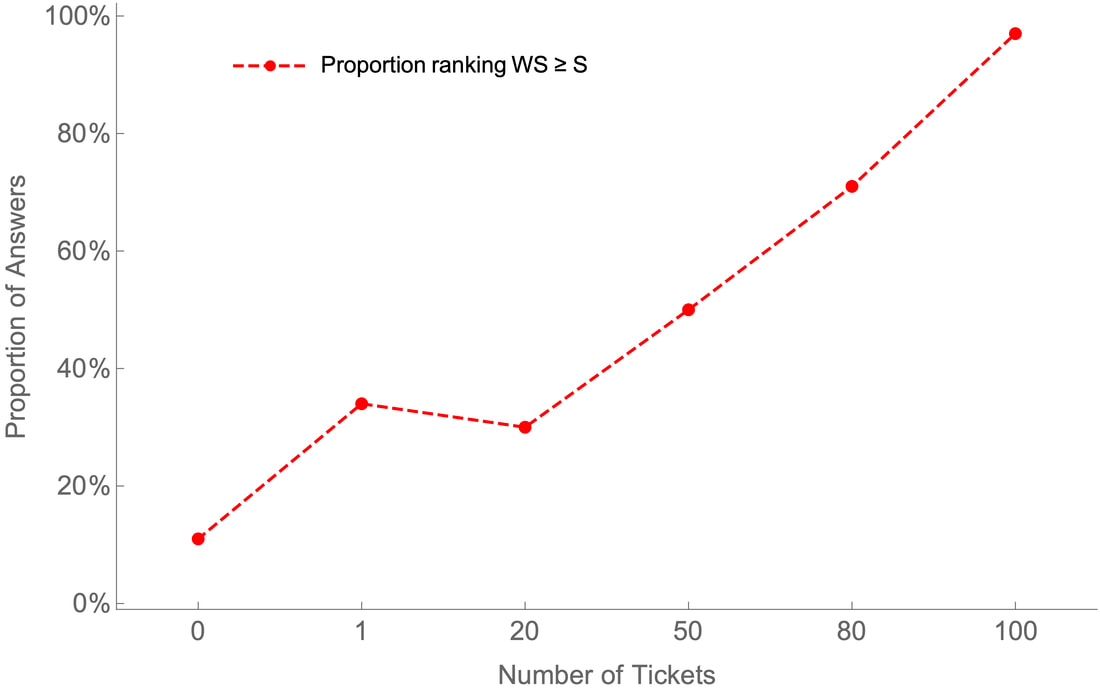
In particular, our model of expected answer value predicts that you should rate “feminist bank teller” as a better guess than “bank teller” whenever you’re sufficiently confident that Linda is a feminist given that she’s a bank teller––whenever P(F|T) is sufficiently high, where the threshold for “sufficient” is determined by how much you value being informative (see the Appendix). Why is this conditional probability P(F|T) what matters? Because although the probability of “feminist bank teller” is always less than that of “bank teller”, how much less is determined by this conditional probability, since P(FT) = P(T)•P(F|T). Thus when P(F|T) is high, switching from "bank teller" to "feminist bank teller" has only a small cost to accuracy––which is easily outweighed by the gain in informativity. Our account therefore makes the following prediction: Prediction: Rates of ranking the conjunction AB as more probable than the conjunct B will tend to scale with P(A|B). This prediction is borne out by the data; a clean example comes from Tentori and Crupi (2012). They give a vignette in which they introduce Mark, and then say that he holds X tickets in a 100-ticket raffle––where X varies between 0 and 100 across different experimental conditions. They then ask subjects which of the following is more likely: a) Mark is a scientist and will win the lottery.
The rates of ranking “scientist and will win the lottery” (WS) as more likely than (or equally likely as) “scientist” (S) scaled directly with the number of tickets Mark held, i.e. with the probability that Mark wins the lottery given that he’s a scientist, P(W|S) (which equals P(W), since S and W are independent):
This is exactly what the answer-value account predicts.
(800 words left)
4. So is the conjunction fallacy irrational?
Suppose the answer-value account is right: people commit the conjunction fallacy when they rate answers for their quality as guesses rather than for their probability of being true. What would that imply about the conjunction fallacy, and its role in the debate about human rationality more broadly? The answer is subtle. One the one hand, it turns out that questions like “What do you think is (most) likely?” are standard ways of eliciting guesses––which in turn have a very different normative profile than probability judgments. For example, when we asked “Who do you think will win?” in our opening question, answering “Pence” is not irrational––nor would it be so if we tweaked the wording to “What’s most likely?”; “What do you bet will happen?”; etc. These are all ways of eliciting guesses. (Note: our second Twitter poll used "What do you think's likely to happen?") Since these prompts are standard ways of eliciting answers in conjunction-fallacy experiments, this complicates our assessment of such answers. The pragmatic upshot of the question that’s being asked is not a literal question about probability: people will hear these questions are requests to guess—to trade off probability against informativity––rather than to merely assess probability. And reasonably so. On the other hand, using such guesses to guide your statements and actions can lead to mistakes. This is clearest in experiments that elicit the conjunction fallacy while asking people to bet on options. Of course, “What do you bet will happen?” is a natural way of eliciting a guess in conversation (“I bet Pence’ll win”). Nevertheless, if we actually give you money and you choose to let it ride on “Pence or Carlson” rather than “Pence, Carlson, or Haley”, then you’ve made a mistake. Moreover, experiments show that people do have a tendency to bet like this––though the rates of the fallacy diminish somewhat. In scenarios like this, the conjunction fallacy is clearly a mistake. The crucial question: What does this mistake reveal about human reasoning? If our account is right, it does not reveal––as is commonly claimed––that human judgment works in a non-probabilistic way. After all, what’s happening is that people are guessing and then acting based on that guess––and guessing requires an (implicit) assessment of probability. Instead, the conjunction fallacy reveals that people are bad at pulling apart judgments about pure probability from a much more common type of judgment––the quality of a guess. Why are people bad at this? Our proposal: because guessing is something we do all the time. Moreover, it’s something that makes sense to do all the time. We can’t have degrees of belief about all possibly-relevant claims––no system could, since general probabilistic inference is intractable. So instead, we construct probability judgments about the small set of claims generated by the question under discussion, use them to formulate a guess, and then reason within that guess. There’s empirical evidence that people do this. For example: poker players decide what to bet by guessing what hands their opponents might have; doctors decide what tests to perform by guessing their patients' ailments; scientists decide what experiments to run by guessing which hypothesis is true; and so on. People do this, we think, because probability alone doesn’t get you very far. The most probable answer is always, “Something will happen, somewhere, sometime.” Such certainly-true answers don’t help guide our actions––instead, we need to trade off such certainty for some amount of informativity. If this is right, the error revealed by the conjunction fallacy is in some ways like that revealed by the Stroop test. Watch the following video and try––as quickly as possible––to say aloud the color of the text presented (do not read the word): It’s hard! And the reason it’s hard is that it requires doing something that you don’t normally do: assess the color of a word without reading it. Yet throughout most of life, what you do when presented with a word––what makes sense to do––is read it. In short: a disposition that involves sophisticated processing, and is rational in general, can lead to errors in certain cases. Likewise, it’s hard not to commit the conjunction fallacy because that requires doing something that you don’t normally do: assess the probability of an uncertain claim without assessing it as a guess. Yet throughout most of life, what you do when presented with such a claim––what makes sense to do––is assess its quality as a guess. In short: a disposition that involves sophisticated processing, and is rational in general, can lead to errors in certain cases. Upshot: although the conjunction fallacy is sometimes a mistake, it is not a mistake that reveals deep-seated irrationality. Instead, it reveals that when forming judgments under uncertainty, we need to trade off accuracy for informativity––we need to guess. What next? If you enjoyed this post, please consider retweeting it, following us on Twitter (Kevin, Matt), or signing up for the newsletter. Thanks! If you’re interested in the details, including other potential applications of guessing to epistemology, philosophy of language, and cognitive science, check out the full paper. If you want to learn more about guessing, also check out this paper by Ben Holguín, this one by Sophie Horowitz, or this classic by Kahneman and Tversky. If you want to learn more about the conjunction fallacy, Tversky and Kahneman’s original paper is fantastic, as is this 2013 paper by Tentori et al.––which provides a good overview as well as its own interesting proposal and data. Appendix Here we’ll state some of the core ideas a bit more formally; see the full paper for the details. How can we generalize our observations about good and bad guesses? Recall that we can model a question as the set of it’s complete answers: “Who will win the nomination?” corresponds to {Pence will win, Carlson will win, Haley will win}. Our two most important observations about good guesses come from Holguín’s paper: Filtering: A guess is permissible only if it is filtered: if it includes a complete answer q, it must include all complete answers that are more probable than q. This explains the answers (4)–(6) that sound odd. “Carlson” (of course) includes “Carlson” but omits the more probable “Pence”. “Carlson or Haley” does likewise. Meanwhile, “Pence or Haley” include “Haley” but excludes the more probable “Carlson”. In contrast, the answers that sound natural––“Pence”, “Pence or Carlson”, and “Pence, Carlson, or Haley”––are all filtered. The second observation Holguín makes is that any filtered guess is permissible: Optionality: There is a permissible (filtered) guess that includes any number of complete answers. In other words, it’s permissible for your guess to include 1 complete answer (“Pence”), 2 complete answers (“Pence or Carlson”), or all three (“Pence, Carlson, or Haley”). How does our model of the accuracy-informativity tradeoff explain these constraints? There are two steps. First, true guesses are always better than false guesses, so we’ll assign false guesses an answer-value of 0, while true guesses always get some positive value. That positive value is determined by the (true) guess’s informativity, as well as how much you value informativity (in the given context). Precisely, let the informativity of $p$, $Q_p$, be the proportion of the complete answers to $Q$ that $p$ rules out. Thus relative to the question “Who will win the nomination?”, “Pence” has informativity ⅔, “Pence or Carlson” has informativity ⅓, and “Pence, Carlson, or Haley” has informativity 0. Meanwhile, let $J \ge 1$ be a parameter that captures the Jamesian value of informativity. If $p$ is true, it’s answer-value is $J$ raised to the power of $p$’s informativity: $J^{Q_p}$. Thus the expected answer-value, given question $Q$, value-of-informativity $J$, and probabilities $P$, is:
This formula reveals the accuracy-informativity tradeoff. It’s easy to make the first term (i.e. $P(p)$) large by choosing a trivial truth (“Pence, Carlson, or Haley”), but this makes the second term (i.e. $J^{Q_p}$) small. Conversely, it’s easy to make the second term large by choosing a specific guess (“Pence”), but this makes the first term small. A good guess is one that optimizes this tradeoff between saying something accurate and saying something informative, given your probabilities $P$ and value-of-informativity $J$.
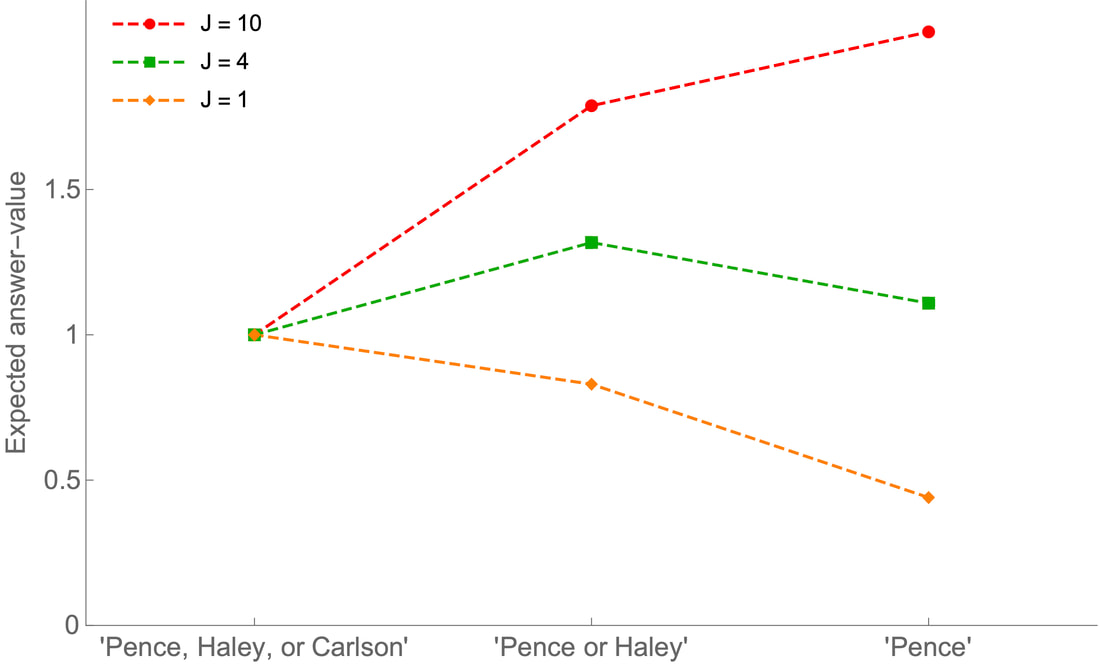
Our proposal: It’s permissible for $p$ to be your guess about $Q$ iff, for some value of $J\ge 1$, $p$ maximizes this quantity $E^J_Q(p)$. This explains both Filtering and Optionality. Filtering is simple. If you choose a non-filtered guess (like “Pence or Haley”), it includes a complete answer that is less probable than an alternative that it excludes (“Haley” is less probable than “Carlson”). Thus by swapping out the latter for the former, we obtain a new guess (“Pence or Carlson”) that is equally informative but more probable––and, therefore, has higher expected answer-value. Optionality takes a bit more work, but the basic idea is simple. When $J$ has the minimal value of 1, being informative carries no extra value ($1^{Q_p} = 1$, no matter what $Q_p$ is)––so the best option is to say the filtered guess that you’re certain of (“Pence, Carlson, or Haley”). But as J grows, informativity steadily matters more and more––meaning that more specific guesses get steadily higher expected answer-values. In our example: when $J < 1.75$, “Pence, Carlson, or Haley” is best; when $6.71 > J > 1.75$, “Pence or Carlson” is best; and when $J > 6.71$, “Pence” is best:
Thus by varying the value or informativity, the accuracy-informativity tradeoff can lead you to guess different filtered answers.
How do we derive our predictions about the conjunction fallacy from this model? We can illustrate this precisely with a simple example (which generalizes). Suppose the question under discussion is the result of crossing “Is Linda a feminist?” ($F$ or $\overline{F}$?) with “Is she a bank teller?” ($T$ or $\overline{T}$?), so the possible complete answers are:
Our model says that you should rank “feminist bank teller” as a better guess than “bank teller” iff it has higher expected answer-value. Since the informativity of "feminist bank teller" is ¾ (it rules out ¾ of the cells of the partition) and the informativity of "bank teller" is ½ (it rules out ½ of the cells), our above formula implies that the expected answer-value of the former is higher than that of the latter iff:
That is: you should guess that Linda is a “feminist bank teller” over “bank teller” whenever you are sufficiently confident that Linda is a feminist given that she’s a bank teller––where the threshold for “sufficient" is determined by the value of informativity, J.
For example, if you’re 80% confident she’s a feminist, independently of whether she’s a bank teller, then this condition is met iff $P(F|T) = P(F) = 0.8 > \frac{1}{J^{¼}}$, iff $J>2.44$. (Compare: in our original example, you should guess “Pence” iff $J > 6.71$.) Thus we expect the conjunction fallacy to be common in the Linda scenario so long as they are sufficiently confident that Linda is a feminist, given that she’s a bank teller––as seems reasonable, given the vignette.
13 Comments
Peter Gerdes
7/18/2020 02:08:33 pm
This was really great. There isn't enough work that doesn't just debate which label to give behavior but makes substantive and plausible hypothesises about why that behavior is seen.
Reply
Peter Gerdes
7/18/2020 02:25:07 pm
For an explicit example consider the following question. A computer program simulates the rolling of 1000 six sided dice and reports only two pieces of information: if at least one 1 was rolled and if at least 1 two was rolled. Since we again have two outcomes
Reply
Kevin
7/20/2020 03:00:02 am
Thanks Peter!
Reply
Stanley Dorst
7/18/2020 02:57:15 pm
This is a very interesting proposal, and I think it makes a lot of sense. From a psychological perspective, another aspect to these questions is that, in order to answer them with the probabilistically "correct" response, one has to ignore some of the information given in the question. In the election problem, one has to ignore the explicitly stated fact that Haley has a much smaller chance of winning than either of the other two. This is even more of an issue in the bank teller problem, where almost all of the information given about the woman is irrelevant to whether or not she is a bank teller, while most of it is quite relevant to whether or not she is a feminist. I think we intuitively assume that the information we are given is intended to be relevant to the question we are asked. When, as in the bank teller case, it is all a red herring, we are likely to give the "wrong" answer.
Reply
Kevin
7/20/2020 03:06:42 am
Totally! This is a good point that helps motivate a bunch of alternative, not irrationality-based explanations. On our story, the relevance point could be used to put some pressure on what the relevant question-under-discussion is, and/or how much you should value informativity. There are other accounts of the CF based on "implicature" (reading between the lines of the answers and the question), which empirically seem to account for some of the data, and would explain why you "read between the lines" by appeal to the considerations of relevance you bring up.
Reply
Eric Mandelbaum
7/22/2020 05:33:42 pm
Hey Matt & Kevin. Wondering how/whether you want to extend this analysis to other failures that sometimes fall under the conjunction fallacy label, but seem, at least to my eyes, less amenable to your (totally reasonable) guessing idea. What I have in mind are examples like:
Reply
Kevin
7/23/2020 08:29:02 am
Thanks for the great question, Eric! We definitely think there are multiple different things going on in many (probably all) of these cases, and I think we agree that the examples you bring up might be ones where other mechanisms do more of the work. That certainly seems to be true for the -_n_ vs. -ing cases, to us. I think we totally buy that the latter makes the search for examples easier (it gives you/primes you with information for where to look). I'm inclined to think whether that one counts as irrational is super subtle (I sort of like this "Bayesian sampler" idea that Chater and others have written about recently––though I suspect you're skeptical!).
Reply
EM
7/23/2020 09:36:17 am
Thanks for the reply. One reason to think that the dice rolling case is going to be hard to gloss as rational is just that if you flip the options a bit people won't make the mistake anymore. Delete the last roll from option two and insert the first one and no one is picking option 2 over option 1 anymore. However we specify the QUD it's presumably the same in both cases.
Kevin
7/25/2020 04:49:03 am
Got it, yeah that makes sense. I think I agree with you that it's much easier make the case for the (1) approach than the (2) one! In diving into this literature Matt and I got pretty convinced that we're not going to get a fully rational explanation of what's going on---I mean, some cases are just clear mistakes, in at least some sense. The betting cases are; and it seems like the dice case probably is too. I do think that there may be certain pictures/explanations of those mistakes that make them seem (in some sense to be made precise) *less* irrational than the standard H&B explanations; but I definitely agree that we're not going to find a full rational vindication here.
Matthew Mandelkern
7/23/2020 11:37:32 am
Hi Eric, thanks for your comments. I agree with all of this basically. The only other thought is that in the die cases, I've always had the worry that people just don't notice the inclusion relations.
Reply
EM
7/23/2020 12:39:03 pm
Oh I agree that they probably don't notice the inclusion relations in the dice case--that's part of why it seems like an irrational mistake to me (and not say a behavior that stems from their Bayesian competence)
Reply
8/5/2020 02:03:21 am
What would this account make the scenario where group deliberation erodes the number of people who commit to the conjunction fallacy?
Reply
Neil Levy
8/31/2020 06:15:30 pm
Very interesting, and I'm sympathetic. One question: what explains (systematic) individual differences in propensity to commit the conjunction fallacy? For example, scores on the CRT predict likelihood of committing the fallacy. If the CRT measures components of good thinking (as is near universally held) and it predicts liability to commit the fallacy, then there's prima facie reason to think that the fallacy itself reflects difficulties with rational processing (I've mentioned the CRT only because I know the literature well; I'm reasonably confident that the correlation also holds with other bad stuff; e.g Brotherton and French find it correlates with conspiratorial thinking).
Reply
Leave a Reply. |
Kevin DorstPhilosopher at MIT, trying to convince people that their opponents are more reasonable than they think Quick links:
- What this blog is about - Reasonably Polarized series - RP Technical Appendix Follow me on Twitter or join the newsletter for updates. Archives
June 2023
Categories
All
|
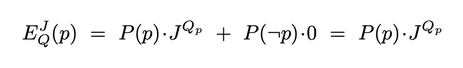
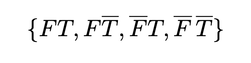
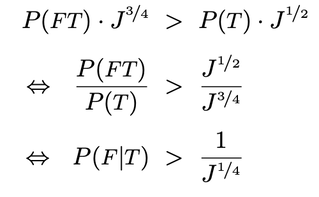
 RSS Feed
RSS Feed