How (Not) to Test for Algorithmic Bias (Guest Post)

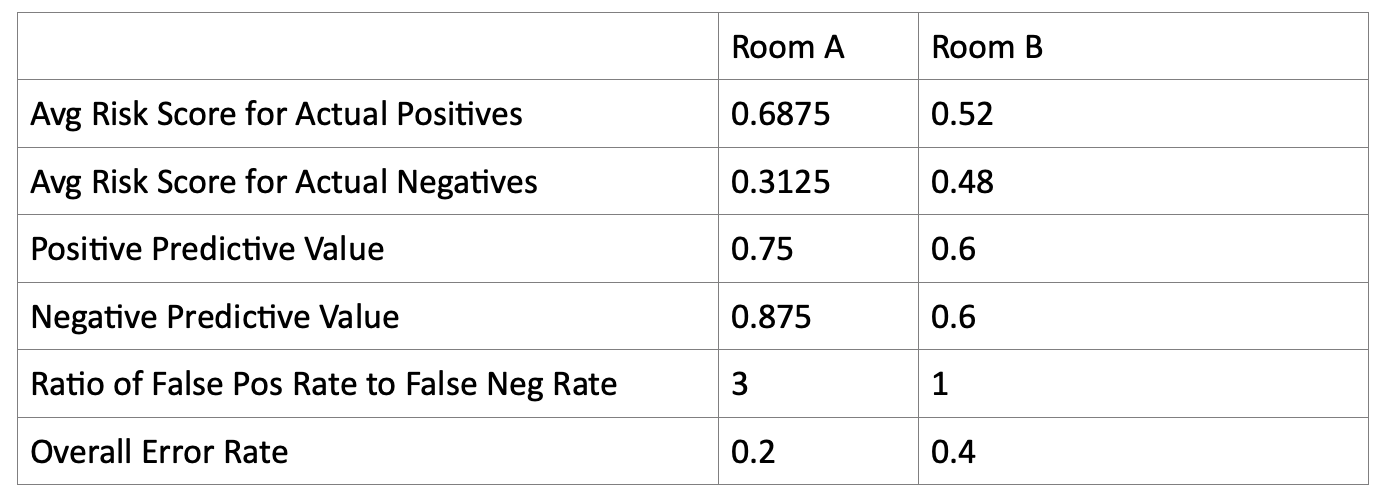
This is a guest post by Brian Hedden (University of Sydney).
(3000 words; 14 minute read)

Predictive and decision-making algorithms are playing an increasingly prominent role in our lives. They help determine what ads we see on social media, where police are deployed, who will be given a loan or a job, and whether someone will be released on bail or granted parole. Part of this is due to the recent rise of machine learning. But some algorithms are relatively simple and don’t involve any AI or ‘deep learning.’

As algorithms enter into more and more spheres of our lives, scholars and activists have become increasingly interested in whether they might be biased in problematic ways. The algorithms behind some facial recognition software are less accurate for women and African Americans. Women are less likely than men to be shown an ad relating to high-paying jobs on Google. Google Translate translated neutral non-English pronouns into masculine English pronouns in sentences about stereotypically male professions (e.g., ‘he is a doctor’).

When Alexandria Ocasio-Cortez noted the possibility of algorithms being biased (e.g., in virtue of encoding biases found in their programmers, or the data on which they are trained), Ryan Saavedra, a writer for the conservative Daily Wire, mocked her on Twitter, writing “Socialist Rep. Alexandria Ocasio-Cortez claims that algorithms, which are driven by math, are racist.”

I think AOC was clearly right and Saavedra clearly wrong. It’s true that algorithms do not have inner feelings of prejudice, but that doesn’t mean they cannot be racist or biased in other ways.

​But in any particular case, it’s tricky to determine whether a given algorithm is in fact biased or unfair. This is largely due to the lack of agreed-upon criteria of algorithmic fairness.

This lack of consensus can be usefully illustrated by the controversy over the COMPAS algorithm used to predict recidivism. (It’s so famous that the Princeton computer scientist Arvind Narayanan jokes that it’s mandatory to mention COMPAS in any discussion of algorithmic fairness!)

In a major report for ProPublica, researchers concluded that COMPAS is ‘biased against blacks,’ to quote the headline of their article. They reached this conclusion on the grounds that COMPAS yielded a higher false positive rate (non-recidivists incorrectly labelled high-risk) for black people than for white people, and a higher false negative rate (recidivists incorrectly labelled low-risk) for white people than for black people.

Northpointe, the company behind COMPAS, responded to ProPublica’s charge, noting that COMPAS was equally accurate for black and white people, in the sense that their risk scales had equal AUC’s (areas under the ROC curve). (Roughly, the AUC, applied to the case at hand, represents the probability that a random recidivist will be ranked as lower risk than a random non-recidivist. I won’t get into the technical details of this concept, but see here for some background.) And Flores, Bechtel, and Lowenkamp defended COMPAS on the grounds that, for each possible risk score, the percentage of those assigned that risk score who went on to recidivate was roughly the same for black and for white people.

It seems that ProPublica was tying fairness to one set of criteria, while Northpointe and Flores et al. were tying fairness to a different set of criteria. How should we decide which side was right? How should we decide whether COMPAS was really unfair or biased against black people? More generally, how should we decide whether an algorithm is unfair or biased?

​Before jumping into this discussion, it’s worth pointing out that the debate over algorithmic fairness also bears on the fairness of human predictions and decisions. We can, after all, think of human prediction and decision-making as based on an underlying algorithm. And some possible criteria for what it takes for an algorithm to be fair, including those we’ll focus on below, can be applied to any set of predictions or decisions whatsoever, regardless of the nature of the underlying mechanism that produces them.

2400 words left

Statistical Criteria of Fairness
Let’s focus on algorithms like COMPAS. These algorithms make predictions, not decisions, though of course their predictions might be used to feed into decisions about bail, parole, and the like. The algorithms in question take as input a ‘feature vector’ (a set of known characteristics) and output either a risk score, or a binary prediction, or both. For simplicity, let’s focus on algorithms that output both a real-valued risk score between 0 and 1 and a binary (yes/no) prediction. We can think of the risk score as a probability that the individual will fall into the ‘positive’ class, and the prediction as akin to a binary belief about whether the individual will be positive or negative.

What criteria must a predictive algorithm satisfy in order to qualify as fair and unbiased? Some criteria concern the inner workings of the algorithm. Perhaps a fair algorithm must not use group membership as part of the feature vector upon which its predictions are based. It must be blinded to whether the individual is male or female, black or white, and so on. Perhaps fairness also requires that the algorithm be blinded to any ‘proxies’ for group membership. For instance, we might regard ZIP code as a proxy for race, given that housing in the US is highly segregated. It is a difficult matter to say in general when some feature counts as a proxy in a problematic sense, but the basic idea is clear enough.

Fairness also presumably requires that the algorithm use the same threshold in moving from a risk score to a binary prediction. It would be unfair, for instance, if black people assigned a risk score above 0.7 were predicted to recidivate, while only white people assigned a risk score above 0.8 were predicted to recidivate. These criteria are relatively uncontroversial and relatively easy to satisfy (except for the tricky issue of proxies for group membership). But are there any other criteria that an algorithm must satisfy in order to be fair and unbiased?

This post will be concerned with a class of purported fairness criteria that require that certain relations between predictions and actuality be the same across the relevant groups. I’ll call these ‘statistical criteria of fairness.’ These are the sorts of criteria that are at issue in the debate over COMPAS. They are of interest in part because we can determine whether they are satisfied by some algorithm just by looking at what it predicted and what actually happened. We don’t need to look at the inner workings of the algorithm, which may be proprietary or otherwise opaque. (This opacity is itself a problem, and we should seek as much transparency as possible going forward.)

Here are the main statistical criteria of fairness at issue in the debate over COMPAS. See the Appendix for several more that have been considered and discussed in the literature.

(1) Calibration Within Groups: For each possible risk score, the percentage of individuals assigned that risk score who are actually positive is the same for each relevant group and equal to that risk score.
(2) Equal False Positive Rates: The percentage of actually negative individuals who are falsely predicted to be positive is the same for each relevant group
(3) Equal False Negative Rates: The percentage of actually positive individuals who are falsely predicted to be negative is the same for each relevant group.

It’s pretty easy to see why each seems like an attractive criterion of fairness. If an algorithm violates (1) Calibration Within Groups, then it would seem that a given risk score has different evidentiary value for members of different groups. A given risk score would ‘mean’ different things for different individuals, depending on which group they are members of. If an algorithm violates (2), yielding a higher false positive rate for one group than for another, it’s tempting to conclude that it was being more ‘risky,’ or was jumping to conclusions more quickly, with respect to one group versus another. The same goes if it violates (3), yielding a higher false negative rate for one group than for another. And this seems unfair. It seems to conflict with the idea that individuals should be treated the same by the algorithm, regardless of their group membership.

1700 words left

Impossibility Theorems
It would be nice if some algorithms could satisfy all of these criteria. This wouldn’t mean that the algorithm is in fact fair. Even if each of these statistical criteria is necessary for fairness, they are not jointly sufficient – we saw above that there are additional, non-statistical criteria that must be satisfied as well. But still, it would be a promising start if an algorithm could satisfy all of these statistical criteria.

But it is impossible for an algorithm to satisfy all of these criteria, except in marginal cases. This is the upshot of a series of impossibility theorems. Two such theorems are particularly important. Kleinberg et al. prove that no algorithm can jointly satisfy (1) and close relatives of (2) and (3) unless either (i) base rates (i.e. the percentage of individuals who are in fact positive) are equal across the relevant groups, or (ii) prediction is perfect (i.e. the algorithm assigns risk score 1 to all positive individuals and 0 to all negative individuals).  Chouldechova proves that no algorithm can jointly satisfy (2) and (3) and a close relative of (1), again unless base rates are equal or prediction is perfect.

I won’t go through the proofs of these impossibility theorems, but they’re not terribly technical. And here’s a great explanation of the theorems and their importance.

​What should we make of these theorems? Pessimistically, we might conclude that fairness dilemmas are all but inevitable; outside of marginal cases, we cannot help but be unfair or biased in some respect.

​More optimistically, we might conclude that some of our criteria are not in fact necessary conditions on algorithmic fairness, and that we need to take a second look and sort the genuine fairness conditions from the specious ones. This is the tack I will take.

1400 words left

People, Coins, and Rooms
How could we go about determining which (if any) of the above statistical criteria are genuinely necessary for fairness? One methodology would be to go one-by-one, looking at the motivations behind each criterion, and seeing if those motivations stand up to scrutiny.

Another methodology would be to find a perfect, 100% fair algorithm and see if that algorithm can violate any of those criteria. If it can, then this means that the criterion isn’t necessary for fairness. (If it can’t, this doesn’t mean that the criterion is necessary for fairness; perhaps some other 100% fair algorithm can violate it.) But this methodology may seem unpromising. It would be hard, if not impossible, to find any predictive algorithms that everyone agrees is perfectly, 100% fair.

At least, that is the case if we consider algorithms that predict important, messy things like recidivism and professional success. But we can do better by considering coin flips; this will enable us to make use of this second methodology.

Here is the setup: There are a bunch of people and a bunch of coins of varying biases (i.e. varying chances of landing heads). The people are randomly assigned to one of two rooms, A and B. And the coins are randomly assigned to people. So each person has one coin and is in one of our rooms. Our aim is to predict, for each person, whether her coin will land heads or tails. That is, we are trying to predict, for each person, whether they are a heads person or a tails person. Luckily, each coin comes helpfully labelled with its bias.

Here is a perfectly, 100% fair algorithm: For each person, take their coin and read its labelled bias. If the coin reads ‘x’, assign it a risk score of x. If x>0.5, make the binary prediction that it will land heads. If x<0.5, make the binary prediction that it will land tails. (I assume, for simplicity, that none of the coins are labelled ‘0.5.’)

It should be clear that this algorithm is perfectly, 100% fair. This, I think, is bedrock. It’s certainly an odd setup, and there’s some unfortunate randomness, but there’s no unfairness anywhere in the setup––and in particular not in our algorithm itself.

Let’s see how our criteria shake out with respect to this algorithm. A first thing to note is that criteria (1)-(3) were formulated in terms of what outcomes actually result. But with coin flips, anything can happen. No matter how biased a coin is in favour of heads (short of having heads on both sides), it can still land tails, and vice versa. So it’s actually quite easy for our algorithm to violate all of (1)-(3), given the right assignment of coins to people and people to rooms.

This suggests that we should have formulated our criteria in expectational or probabilistic terms:

(1*) Expectational Calibration Within Groups: For each possible risk score, the expected percentage of individuals assigned that risk score who are actually positive is the same for each relevant group and equal to that risk score.
(2*) Expectational Equal False Positive Rates: The expected percentage of actually negative individuals who are falsely predicted to be positive is the same for each relevant group.
(3*) Expectational Equal False Negative Rates: The expected percentage of actually positive individuals who are falsely predicted to be negative is the same for each relevant group.

(There’s a tricky question about how to understand the probability function relative to which these expectations are determined. I’ll think of it as an evidential probability function which represents what a rational person who knew about the workings of the algorithm would expect.)

We can investigate whether our perfectly, 100% fair algorithm can violate any of these starred criteria by considering a case where coin biases match relative frequencies (i.e. exactly 75% of the coins labelled 0.75 land heads, and so on). If our algorithm violates one of the unstarred criteria in this case, then it also violates the starred version of that criterion.

It turns out that our perfectly, 100% fair algorithm must satisfy (1*), but it can violate (2*) and (3*), given the right assignment of coins to people and people to rooms. Moreover, it can violate them simultaneously. And surprisingly, it can violate them simultaneously even when base rates are equal across the two rooms.

The following case illustrates this: Room A contains 12 people with coins labelled ‘0.75’ and 8 people with coins labelled ‘0.125.’ The former are all assigned risk score 0.75 and predicted to be heads people (positive), and nine of them are in fact heads people. The latter are all assigned risk score 0.125 and predicted to be tails people (negative), and seven of them are in fact tails people. Room B contains 10 people with coins labelled ‘0.6’ and 10 people with coins labelled ‘0.4.’ The former are all assigned risk score 0.6 and predicted to be heads people, and six of them are in fact heads people. The latter are all assigned risk score 0.4 and predicted to be tails people, and six of them are in fact tails people.

Note that base rates are equal across the two rooms: exactly ten out of the twenty people in each room are heads people.

While our algorithm in this case satisfies (1) Calibration Within Groups, and hence also (1*), it violates (2) and (3), and hence also (2*) and (3*). For Room A, the False Positive Rate is 3/10, while for Room B it is 4/10. And for Room A, the False Negative Rate is 1/10, while the False Negative Rate is 4/10. This fair algorithm also violates a host of other statistical criteria of fairness that have been suggested in the literature – see the Appendix for details.

​This means that it is possible for a perfectly, 100% fair algorithm to violate (2*) and (3*) when given the right population as input. This suffices to show that neither is a necessary condition on fairness. It also suffices to show that none of the other criteria considered in the Appendix are necessary for fairness, either. Only (1*) Expectational Calibration Within Groups is left standing as a plausible necessary condition on fairness.

300 words left

Upshots
I think (1*) Expectational Calibration Within Groups is plausibly necessary for fairness. I also think fairness might require that the ‘inner workings’ of the algorithm be a certain way, for instance that the algorithm be blinded to group membership and that it use the same threshold in going from a risk score to a binary prediction. There may be other necessary conditions as well.

But it is misguided to focus on any of the other statistical criteria of fairness considered here or in the Appendix. Those criteria are tempting due to the relative ease of checking whether they are satisfied. But we have seen that an algorithm’s violating those criteria doesn’t mean that the algorithm is in any way unfair.

Now, even a perfectly fair predictive algorithm might have troubling results when used to make decisions in a certain way. It might have a disparate impact on the relevant groups. But the right way to respond to this disparate impact will often be not to modify the predictive algorithm, but rather to modify the way decisions are made on the basis of its predictions, or to intervene in society in other ways, for instance through reparations, changes in the tax code, and so on.

​Of course, some of these responses might be politically infeasible. This is especially true for some of the policies that might be most effective in redressing racial and other injustices. Reparations would be a case in point. It is difficult to imagine reparations becoming policy, despite Ta Nehisi Coates’ influential recent defense. If we can’t deal with racial (or other) injustices in these other ways, perhaps the best response is to chip away at injustice by modifying what was already a fair predictive algorithm. It’s not the ideal solution, but it might be second best. Still, it is important to be clear that an algorithm’s violating Equal False Positive/Negative Rates (or any of the other statistical criteria considered in the Appendix) neither entails nor constitutes the algorithm’s unfairness.


What next?
For an accessible explanation of the impossibility theorems, see this piece on Phenomenal World by Cosmo Grant​.
For the back-and-forth about COMPAS, see the initial ProPublica report,  Northpointe's response, and Propublica's counter-response.
For a more general discussion of the issues surrounding algorithmic fairness, see this article.

Appendix
In this Appendix, I’ll briefly mention some of the other main statistical criteria of fairness that have been considered in the literature:

(4) Balance for the Positive Class: The average risk score assigned to those individuals who are actually positive is the same for each relevant group.
(5) Balance for the Negative Class: The average risk score assigned to those individuals who are actually negative is the same for each relevant group.
(6) Equal Positive Predictive Value: The percentage of individuals predicted to be positive who are actually positive is the same for each relevant group.
(7) Equal Negative Predictive Value: The percentage of individuals predicted to be negative who are actually negative is the same for each relevant group.
(8) Equal Ratios of False Positive Rate to False Negative Rate: The ratio of the false positive rate to the false negative rate is the same for each relevant group.
(9) Equal Overall Error Rates: The number of false positives and false negatives, divided by the number of individuals, is the same for each relevant group.

The first two – (4) and (5) – can be seen as generalizations of (2) and (3) to the case of continuous risk scores. Indeed, Pleiss et al. refer to the measures involved in (4) and (5) as the ‘generalized false negative rate’ and the ‘generalized false positive rate,’ respectively. And, along with (1), it is these two criteria, rather than (2) and (3), that are the target of the aforementioned impossibility theorem from Kleinberg et al.

The next two – (6) and (7) – can be seen as generalizations of (1) to the case of binary predictions. This is how Chouldechova conceives of them. Just as (1) is motivated by the thought that a given risk score should ‘mean’ the same thing for each group, so (6) and (7) can be motivated by the thought that a given binary prediction should ‘mean’ the same thing for each group. Chouldechova’s impossibility result targets (6) rather than (1), showing that (2), (3), and (6) are not jointly satisfiable unless either base rates are equal or prediction is perfect.

The final two – (8) and (9) – are also intuitive. For (8), it would seem that violating this criterion would mean that the relative importance of avoiding false positives versus avoiding false negatives was evaluated differently for the different groups. Finally, (9) Equal Overall Error Rates embodies the natural thought that fairness requires that the algorithm be equally accurate overall for each of the different groups.

​We can now easily see that our perfectly fair predictive algorithm violates all these criteria as well (and hence also their expectational or probabilistic analogues), given the same assignment of coins to people and people to rooms as above:

The fact that the numbers in the Room A column and the Room B column differ for each row means that our fair predictive algorithm violated all of (4)-(9), in addition to (2) and (3). This suffices to show that none of (4)-(9), nor their expectational/probabilistic analogues, is a necessary condition on fairness. Among all these statistical criteria, only (1*) Expectational Calibration Within Groups is left standing as a plausible necessary condition on fairness.