|
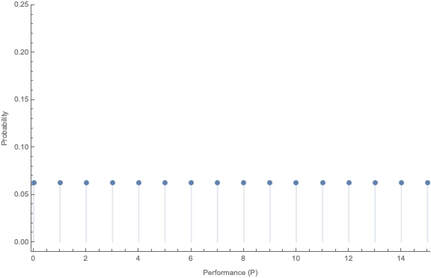
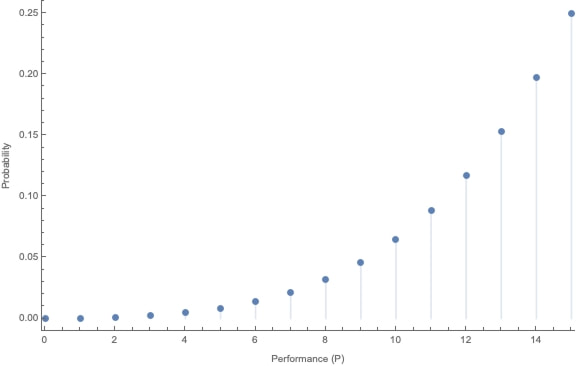
(1700 words; 10 minute read. This post was inspired by a suggestion from Chapter 2 (p. 60) of Jess Whittlestone's dissertation on confirmation bias.) Uh oh. No family reunion this spring—but still, Uncle Ron managed to get you on the phone for a chat. It started pleasantly enough, but now the topic has moved to politics. He says he’s worried that Biden isn’t actually running things as president, and that instead more radical folks are running the show. He points to some video anomalies (“hand floating over mic”) that led to the theory that many apparent videos of Biden are fake. You point out that the basis for that theory has been debunked—the relevant anomaly was due to a video compression error, and several other videos taken from the same angle show the same scene. He reluctantly seems to accept this. The conversation moves on. But a few days later, you see him posting on social media about how that same video of Biden may have been fake! Sigh. Didn’t you just correct that mistake? Why do people cling on to their beliefs even after they’ve been debunked? This is the problem; another instance of people’s irrationality leading to our polarized politics—right? Well, it is a problem. But it may be all the thornier because it’s often rational. Real-world political cases are messy, so let’s turn to the lab. The phenomenon is what’s known as belief perseverance: after being provided with evidence to induce a particular belief, and then later being told that the evidence was actually bunk, people tend to still maintain the induced belief to some extent (Ross et al. 1975; McFarland et al. 2007). A classic example: the debriefing paradigm. Under the cover story of testing subjects’ powers of social perception, researchers gave them 15 pairs of personal letters, and asked them to identify which was written by a real person and which was written by the experimenters. Afterwards, they received feedback on how well they did. Unbeknownst to the subjects, that feedback was bogus—they were (at random) told that they got either 14 of 15 notes correct (positive feedback), or 4 of 15 correct (negative feedback). Both groups were told the average person got 9 of 15 correct. As a result of this feedback, they come to believe that they are above (or below) average on this sort of task. Some time later, subjects are “debriefed”: told that the feedback that they received was bunk, and had nothing to do with their actual performance. They’re then asked to estimate how well they would do on the task if they were to perform it on a new set of letters. The belief perseverance effect is that, on average, those who received the positive feedback expected to do better on a new set of letters than those who received the negative feedback—despite the fact that they had both been told that the feedback they received was bunk! So even after the evidence that induced their belief had been debunked, they still maintained their belief to some degree. And rationally so, I say. Imagine that Baya the Bayesian is doing this experiment. She’s considering how well she’d Perform on a future version of the test—trying to predict the value of a variable, P, that ranges from 1–15 (the number she’d get correct). She doesn’t know how she’d perform, but she can form an estimate of this quantity, E[P]: a weighted average of the various values P might take, with weighs determined by how likely she thinks they are to obtain. Suppose she starts out with no idea—she’s equally confident that she’d get any score between 1–15: Then her estimate for P is just the straight average of these numbers: E[P] = 1/15*1 + 1/15*2 + … + 1/15*15 = 8 Suppose now she’s given positive feedback (“You got 14 of 15 correct!”)—label this information “+F”. Given this feedback, she can form a new estimate, E[P|+F] of how well she’d do on a future test—and since her feedback was positive, that new estimate should be higher than her original estimate of 8. Perhaps, given the feedback, she’s now relatively confident she’d get a good score on the test—her probabilities look like this: Then her estimate for her performance is roughly 13: E[P | +F] ≈ 0.25 *15 + 0.2*14 + 0.15*13 + … = 13 Now in the final stage, she’s told that the positive feedback she received was bunk. So the total information she received is “positive feedback (+F), but told that it was bunk”. What should her final estimate of her future performance, E[P | +F, told bunk], be? Well, how much does she believe the experimenters? After all, they’ve already admitted they’ve lied to her at least once; so how likely does the fact that they told her the feedback was bunk make it that the feedback in fact was bunk? Something less than 100%, presumably. Now, what she was told about whether the feedback was bunk is relevant to her estimate of her future performance only because it is evidence about whether the feedback was actually bunk. Thus information about whether the feedback was bunk should “screen off” what the experimenters told her. (If a hyper-reliable source told her “The feedback was legit—they were lying to you when they told you it was bunk”—she should go back to estimating that her performance would be quite good, since the legitimate feedback was positive.) Upshot: so long as Baya doesn’t completely trust the psychologist’s claim that the information was bunk—as she shouldn’t, since they’re in the business of deception—then she should still give some credence to the possibility that the feedback wasn’t bunk. (800 words left) Crucial point: if she’s unsure whether the feedback she received was bunk, her final estimate for her future performance should be an average of her two previous estimates. Conditional on the feedback actually being bunk, her estimate should revert to it’s initial value of 8: E[P | +F, told bunk, is bunk] = 8. Meanwhile, conditional on the feedback actually being not bunk, her estimate should jump up to it’s previous high value of 13: E[P | +F, told bunk, not bunk] = 13. When she doesn’t know whether the feedback is bunk or not, she should think to herself, “Maybe it is bunk, in which case I’d expect to get only a 8 on a future test; but maybe it’s not bunk, in which case I’d expect to get a 13 on a future test.” Thus (by what’s known as the law of total expectation) her overall estimate should be an average of these two possibilities, with weights determined by how likely she thinks they are to obtain. So, for example, suppose she thinks it’s 80% likely that the psychologists are telling her the truth when they told her the feedback was bunk. Then her final estimate should be: E[P | +F, told bunk] = 0.8*8 + 0.2*13 = 9. This value is greater, of course, than her original estimate of 8. (The reasoning generalizes; see the Appendix below.) By exactly parallel reasoning, if Baya were instead given negative feedback (–F) at the beginning, she would instead end up with an estimate slightly lower than her initial value of 8; say, E[P | –F, told bunk] = 7. As a result, there should be a difference between the two conditions. Even after being told the feedback was bunk, both groups should wonder whether it in fact was. Because of these doubts, those who received positive feedback should adjust their estimates slightly up; those who received negative feedback should adjust them slightly down. Thus, even if our subjects are rational Bayesians, there should be a difference between the groups who received positive vs. negative feedback, even after being told it was bunk: E[P | +F , told bunk] > E[P] > E[P | –F, told bunk]. The belief perseverance effect should be expected of rational people. A prediction of this story is that insofar as the subjects are inclined to trust the experimenters, their estimates of their future performance should be far less affected by the feedback after being told it was bunk than before so. (The more they trust them, the more weight their initial estimate plays in the final average.) This is exactly what the studies find. For subjects who are never told that the feedback was bunk, those who received negative feedback estimated their future performance to be 4.46, while those who received positive feedback estimated it to be 13.18. In contrast, for subjects who were told the feedback was bunk, those who received negative feedback estimated their future performance at 7.96, while those who received positive feedback estimated it at 9.33. There is a statistically significant difference between these two latter values—that’s the belief perseverance effect—but it is much smaller than the initial divergence. As the rational story predicts. Another prediction of this rational story is that insofar as psychologists can get subjects to fully believe that the feedback really was bunk, the belief perseverance effect should disappear. Again, this is what they find. Some subjects where given a much more substantial debriefing—explaining that the task itself is not a legitimate measure of anything (no one can reliably identify the real letters). Such subjects exhibited no belief perseverance at all. Upshot: in the lab, the belief perseverance effect could well be fully rational. Okay. But what about Uncle Ron? Well, obviously real-world cases like this are much more complicated. But it does share some structure with the above lab example. Ron originally had some some (perhaps quite low) degree of belief that something fishy was going on with Biden. He then saw a video which boosted that level of confidence. Finally, he was then told that the video was bunk. So long as he doesn’t complete trust the source that debunks the video, it makes sense for him to remain slightly more suspicious than he was originally. How suspicious, of course, depends on how much he ought to believe that the video really was bunk. But even if he trusts the debunker quite a bit, a small bump in suspicion will remain. And if he sees a lot of bits of evidence like this, then even if he’s pretty confident that each one is bunk, his suspicions might reasonably start to accumulate. If that's right, the fall into conspiracy theories is an epistemic form of death-by-a-thousand-cuts. The tragedy is that rationality may not guard against it. What next? If you liked this post, consider sharing it on social media or signing up for the newsletter. For more on belief perseverance, check out the recent controversy over the "backfire effect"—the result that sometimes people double-down on their beliefs in the face of corrections. See e.g. Nyhan and Reifler 2010 for the initial effect, and then Wood and Porter 2019 for a replication attempt that argues that the effect is very rare. For more discussion, see the reddit thread on this post. Appendix Consider the Baya case. Why does the reasoning go through generally? P is a random variable—a function from possibilities to numbers—that measures how well she would do on a test if she were to retake it. Given her (probabilistic) credence function C, her estimate for P is In general, her conditional estimate for P, given information X, is: Here are the needed assumptions for the above reasoning to go through. First, information about whether the feedback was bunk screens off whether she was told it was bunk from her estimate about P: and What should her estimate be in those two cases? Well, conditional on the feedback but also it being bunk, she should revert to her initial estimate E[P]: Conditional on it not being bunk, she should move her estimate in the direction of the feedback—so if the feedback is positive, she should raise her estimate of her performance: But of course she doesn’t know whether it was bunk or not—all she knows is that she was told it was bunk. By the law of total expectation, and then our screening off assumption, we have: By parallel reasoning, if she gets negative feedback she should end up with a lower estimate than her initial one: And thus, whenever she doesn’t completely trust the experimenters when they tell her the info is bunk, the feedback should still have an effect: Which, of course, is just the belief perseverance effect.
12 Comments
Peter Gerdes
4/3/2021 03:47:08 pm
That argument's way too fast. You can't just assume that the probability distribution given Told got 14/15 & told was lie & was lie is the same as the probability distribution given no information.
Reply
Kevin
4/4/2021 01:11:35 pm
Thanks for the thoughts!
Reply
Eric
4/5/2021 09:15:13 am
Hi, Kevin,
Reply
Kolja Keller
4/7/2021 08:16:50 am
I'm not Kevin, but I agree with what he says here and the general project, so I have a view on the upshost: First, psychologists need to stop being blunt externalists about rationality when they're testing who is and isn't irrational. That way they're not mislabeling phenomena as irrational that aren't.
Reply
Eric
4/7/2021 02:48:48 pm
Interesting ideas. Though I will say the promise of your sketched alternative panning out are dubious. That interview I linked to in my original post showcases the failure of just the sort of granular deliberations you offer as a viable alternative to "fact-checking". And it seems like such failures are not strictly speaking rational but rather a non-cognitive commitment to a belief state.
Kevin
4/7/2021 06:13:57 pm
Thanks both! Super great questions/comments. I don't have any super easy answers, though I'm definitely inclined to agree with the main points that Kolja mentioned—we at least want to make sure we're understanding the causes of the phenomenon properly, if we're to combat it.
David
4/7/2021 02:01:25 pm
I just wanted to say that while this is a great explanation as to how people get to the wrong conclusion I still feel it is irrational, if you find out that the examiner is unreliable then the rational conclusion you can draw is exactly that and without some other information not provided in the scenario, then there isn't any reason any information they have provided should be used, leaving you with only your original E[P] estimate.
Reply
Kevin
4/7/2021 06:17:22 pm
Thanks for the comment!
Reply
Nathan
4/9/2021 06:57:14 pm
In other words, because we must take the source at their word for the claim's truth, the claim's credibility becomes indexed to the credibility of its source, instead of a situation where each claim can have its own freestanding credibility rating. Even if we know we can only give a low level of belief to a source, because that source's credibility remains above zero it still affects our overall belief. This is only a problem in situations where a claim's credibility MUST be derived from the credibility of its source, something Kolja's proposed solution points out. If we could do a kind of objective catalogue of the evidence in an unbiased way, a kind of "sourceless" presentation, then that might work. But this puts us up against the practical limits of doing a presentation like that for every issue where this problem pops up.
Reply
Kevin
4/10/2021 09:47:13 am
Yeah, I think that's a good way to put it! As information sources get more fast-paced and varied, people can (and have to!) use their own assessments of trustworthiness to filter what to look at and how much to believe it far more than they used to. This leads to all sorts of interesting dynamics, like the fracturing of the media landscape. But it's really a relatively simple (and sensible) mechanism, so it's hard to know how to combat it effectively.
Reply
Emma
5/16/2021 11:40:50 pm
Hi Kevin, thank you for a really interesting article. I know many of us — myself included — have watched loved ones slowly fall prey to disinformation, and felt helpless when they resort to the same conspiracies after deep conversations debunking them.
Reply
Kevin
5/19/2021 10:47:03 am
Hi Emma,
Reply
Leave a Reply. |
Kevin DorstPhilosopher at MIT, trying to convince people that their opponents are more reasonable than they think Quick links:
- What this blog is about - Reasonably Polarized series - RP Technical Appendix Follow me on Twitter or join the newsletter for updates. Archives
June 2023
Categories
All
|
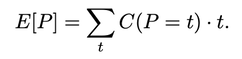
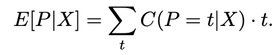
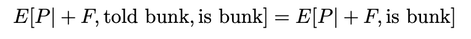
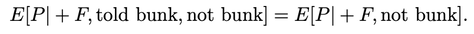
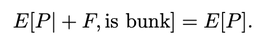
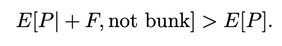

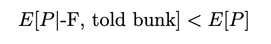
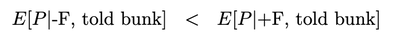
 RSS Feed
RSS Feed